
Оптимизация значений таблицы Excel, удовлетворяющих определенным критериям, может быть сложным процессом. К счастью, Microsoft предлагает надстройку Решение проблем для численной оптимизации. Хотя данный сервис не может решить всех проблем, он может быть полезным в качестве инструмента что-если. Данный пост посвящен надстройке Решение проблем в Excel.
Надстройка Решение проблем доступна во всех версиях Excel. Обратите внимание, что скриншоты могут не соответствовать вашей версии. Несмотря на то, что некоторые функции могут менять свое местоположение в зависимости от версии надстройки, функционал остается практически неизменным.
Что такое Поиск решений
Поиск решений – надстройка Excel, которая помогает найти решение с помощью изменения значений целевых ячеек. Целью может быть минимизация, максимизация или достижение некоторого целевого значения. Проблема решается путем регулировки входных критериев или ограничений, определенных пользователем.
Где в Excel поиск решений
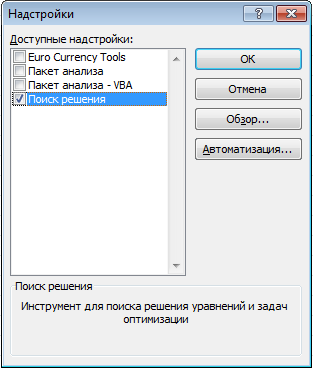
Надстройка Поиск решений поставляется вместе с Excel, но по умолчанию отключена. Чтобы включить его, перейдите по вкладке Файл в группу Параметры. В появившемся диалоговом окне Параметры, выберите Надстройки -> Управление: Надстройки Excel -> Перейти. В окне Надстройки устанавливаем галочку напротив поля Поиск решения, жмем ОК.
Теперь во вкладке Данные появилась новая группа Анализ с кнопкой Поиск решения.
Пример использования Поиска решения
Данный пост основан на примере использования Надстройки Поиск решения. Файл совместим со всеми версиями Excel.
Определение проблемы
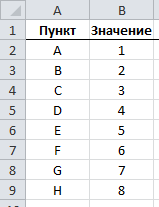
Предположим, что у нас есть набор данных, состоящий из 8 пунктов, каждому из которых соответствует свое значение.
… и нам необходимо скомбинировать значения в две группы так, чтобы суммы значений этих групп примерно совпадали.
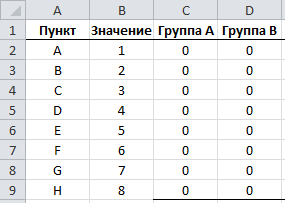
Для начала требуется определить каждый пункт к какой-нибудь группе.
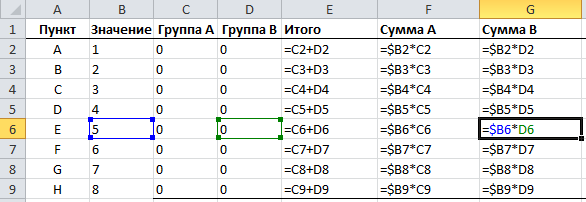
Чтобы указать привязанность пункта к группе, будем помечать их единицей (1), в противном случае нулем (0).
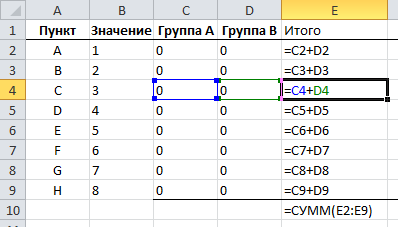
В следующем столбце мы будем суммировать значения каждого пункта в группе, и затем подведем итог в конце столбца.
Нам также необходимо обработать значение каждого пункта в каждой группе, для этого умножаем значение пункта на значение группы, соответствующее этому пункту.
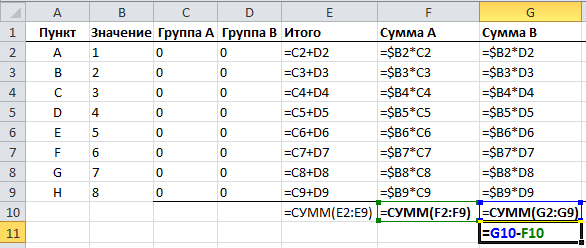
Наконец, нам необходимо свести сумму групп и работать с разницей между ними.
Наша задача минимизировать разницу между суммами групп.
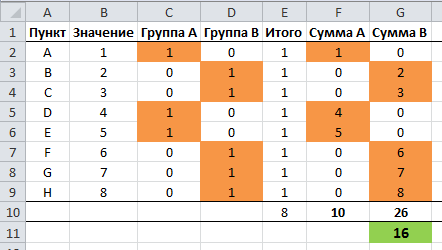
Теперь мы можем присвоить каждой группе пункты, для этого вручную проставляем единицы в столбцах С и D. Excel отобразит разницу сумм групп в ячейке G11.
Для большей наглядности я добавил условное форматирование для ячеек, имеющих значение >0.
Проблема в том, что количество возможных комбинаций 28, т.е. 256 вероятных ответов на вопрос. Если на каждый из них тратить по 5 секунд, это займет у нас 21,3 минуты, предполагая, что мы сможем выдержать темп и запомнить лучшую комбинацию.
Вот где Поиск решения находит применение.
Поиск оптимального решения в Excel
Чтобы применить сервис Поиск решения, нам необходимо определить ряд требований, правил и ограничений, которые позволят надстройке найти правильный ответ.
Наши правила
Наше основное требование – это минимизировать разницу между двумя группами. В нашем примере она находится в ячейке G11 – Группа B минус Группа A. Нам нужно, чтобы значение в ячейке G11 было настолько малым насколько это возможно, но больше или равно 0.
Мы также знаем, что пункт может находиться либо в Группе A, либо в Группе B, к тому он не может быть дробным. Таким образом у нас два ограничения для каждого элемента:
Во-первых: Значение элемента в колонке Итог должна равняться единице.
Во-вторых: Значения элементов в группах должны быть целыми.
Мы также знаем, что общее количество элементов 8, это еще одно ограничение. Как использовать эти ограничения мы обсудим в следующем разделе.
Диалоговое окно Поиска решения
В этом разделе описано окно надстройки Поиск решения и его использования для определения проблемы.
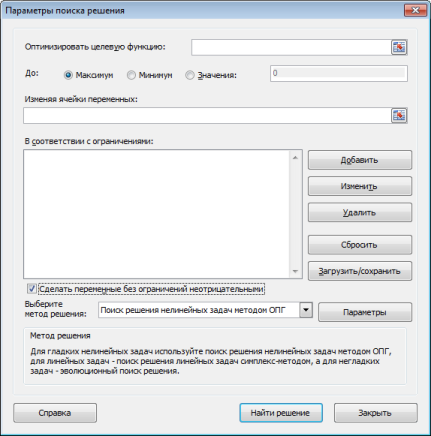
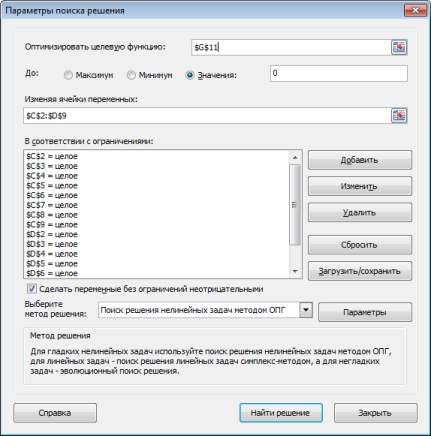
Пустое окно Поиска решения
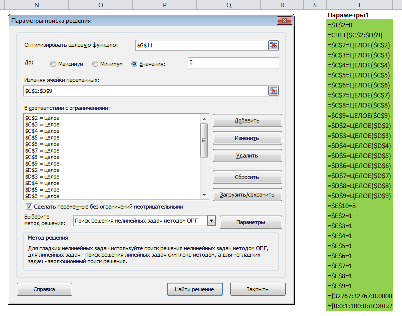
Заполненное окно Поиска решения
Оптимизировать целевую функцию
Это целевая ячейка, в которой мы пытаемся решить проблему. Наша целевая ячейка G11 – разница в группах.
До
Здесь мы указываем, каких результатов хотим добиться от целевой функции.
Мы хотим, чтобы суммы обоих групп совпадали, т.е. чтобы разница сумм была равна 0. Это может показаться странным, но нам не требуется минимизировать разницу, потому что при этом все элементы будут помещены в Группу A, что приведет к значению ячейки G11 меньше нуля.
Другой способ наложения ограничения – изменить G11 на =ABS(G10-F10). При этом мы сможем установить маркер на Минимум, как результат достижения целевой функции.
Но пока мы остановимся на формуле =G10-F10 и установим маркер в значение равным 0.
Изменяя ячейки переменных
Изменяемые ячейки – ячейки, которые надстройка попытается изменить, чтобы решить задачу. В нашем случае это привязка элемента к конкретной группе: $C$2:$D$9.
В соответствии с ограничениями
Ограничения – это правила, которые лимитируют возможные решения проблемы.
Нам необходимо добавить несколько ограничений в наш список:
- В колонке Итого каждый элемент должен равняться 1
- Элементы групп должны быть целым числом
- Сумма значений столбца Итого должна равняться 8
Чтобы наложить ограничения, жмем кнопку Добавить
- Для каждой ячейки диапазона E2:E9 устанавливаем ограничение значения равным 1
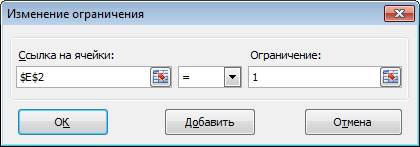
- Для каждой ячейки диапазона C2:D9 устанавливаем ограничение значение целое число.
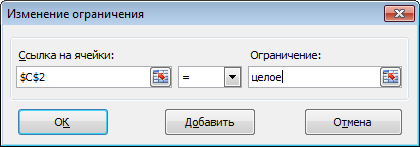
- Необходимо добавить ограничение на сумму обоих групп, ячейка E10 = 8.
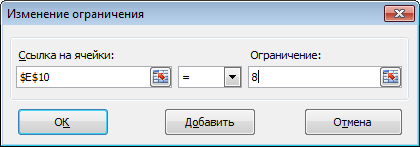
Вы можете Изменить или Удалить ограничение, если допустили ошибку, выбрав конкретное ограничение и нажав соответствующие кнопки в диалоговом окне.
Загрузить/сохранить параметры поиска решений
Сервис поиска решений позволяет сохранять и загружать параметры надстройки. Для этого в окне существует кнопка Загрузить/сохранить. Параметры модели сохраняются в диапазон, который вы указали ранее. Данный подход позволяет быстро настраивать и изменять параметры Поиска решения.
Запуск поиска оптимального решения в Excel
Предупреждение!!! Надстройка поиск решения является сложной вычислительной надстройкой, поэтому перед запуском сохраните рабочую книгу.
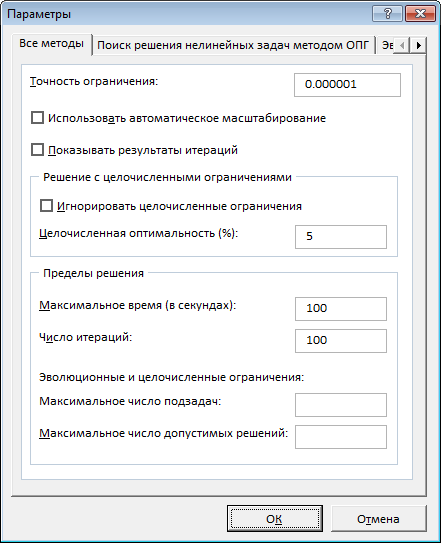
Прежде чем запустить модель, необходимо задать еще несколько параметров, чтобы убедиться, что сервис отработает корректно. В основном диалоговом окне убедитесь, что стоит маркер напротив поля Сделать переменные без ограничений неотрицательными. В этом же окне нажмите кнопку Параметры.
Два параметра, которые необходимо будет менять время от времени:
Точность ограничения: значение от 0 до 1, где, чем больше цифра, тем больше ограничение
Целочисленная оптимальность: показывает насколько далеко от целого числа ограничение имеет право быть.
Запуск модели
Чтобы запустить надстройку нажмите кнопку Найти решение в основном окне.
В строке состояния вы увидите ряд статических данных, которые будут отображать внутреннюю работу надстройки. Как правило, они быстро меняются, и читать их сложно. Если модель сложная, то работа может остановится на некоторое время, надстройка обычно восстанавливается от этих проблем сама.
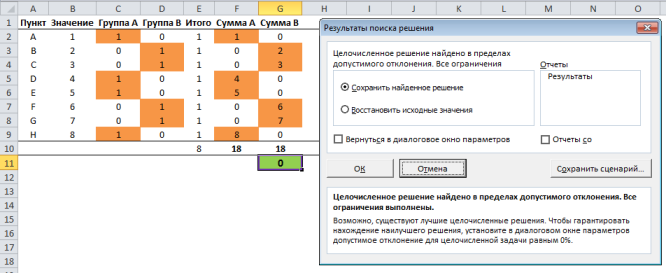
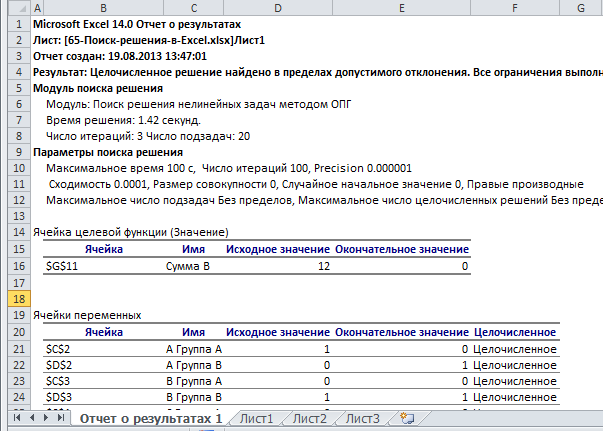
После того, как Поиск решения закончит свою работу, Excel отобразит диалоговое окно Результаты поиска решения с некоторой информацией. Первое, на что стоит обратить внимание – это надпись Решение найдено в пределах допустимого отклонения. Если решение найдено, ячейки рабочей книги изменятся с предложенным решением.
Теперь у вас есть 4 варианта на выбор:
— Запустить отчет
— Сохранить сценарий
— Восстановить исходные значения
— Сохранить найденное решение
Запустить отчет
Вы можете создать отчет, выбрав доступные из списка отчетов. Будет создан новый лист Отчет о результатах1.
Обратите внимание, что в зависимости от установленных вами ограничений, будут доступны различные отчеты.
Сохранить сценарий
Если вы нажмете кнопку Сохранить сценарий, Excel откроет следующее диалоговое окно:
Где необходимо ввести название вашего сценария модели и нажать кнопку ОК.
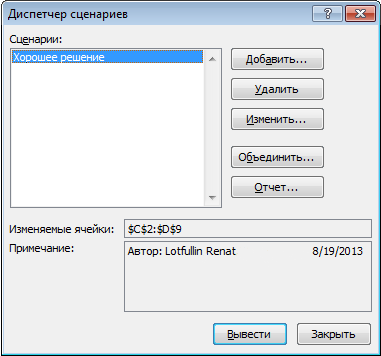
Все сценарии доступны в Диспетчере сценариев, который находится во вкладке Данные в группе Работа с данными –> Анализ что-если -> Диспетчер сценариев.
Вернуться к модели
К тому же, вы можете вернуться к модели и:
— Восстановить исходные значения
— Сохранить найденное решение
Проверка результатов
Сервис Поиск решения, вероятно, самая непредсказуемая система в Excel. Таким образом, все найденные решения, которые он выдает необходимо перепроверять вручную, для дальнейшего использования.
Данная проверка на реалистичность должна начинаться с подтверждения, что все результаты удовлетворяют заданным критериям:
— Являются ли результаты примерно похожими на ваши ожидания?
— Не нарушены ли максимумы и минимумы?

Почему не окрашиваются дубликаты в данном листе?
Файл: 22222.xlsx
Опишите, пожалуйста, методику по которой вы хотели закрасить дубликаты. По вашему файлу трудно разобраться
Спасибо! Быстро разобрался со своей похожей задачей.
как найти поиск решение(((
Файл: -2_ЗАМЕЧ.xlsx
а эту задачу можно решить поиском решения?
———-
В забеге участвуют три лошади: Алла, Бэлла и Виола. Ставки на их победу принимаются с соотношениями 1:1, 1:2 и 1:6 соответственно. Это означает, что если вы, например, поставили на Бэллу, и она пришла первой, то вы получаете
назад свои деньги плюс удвоенную начальную ставку. В противном случае вы теряете деньги. Холмс имеет в кармане 205 фунтов. Может ли он гарантированно
выиграть какую-либо сумму? Если да, то какую?
Типа так?
Файл: .xlsx
нет, не сможет. Тут получается, что сумма выигрыша должна быть больше Суммы затраченной(205 фунтов)- это нереально.
1/2*х+1/3*х+1/7*х=205(целевое значение)
х>205 (ограничение)
находим х=210 (выигранная сумма)
Соответственно ставки:
1) Алла 1/2*х = 1/2*210=105;
2) Бэлла 1/3*х = 1/3*210=70;
3) Виола 1/7*х = 1/7*210=30.
Проверка: 105+70+30=205
Гарантированный выигрыш 210-205=5
В чистом виде эту задачу Поиск решения не «съест». Тут нужно понимать КАК решать чтобы корректно сформулировать условия. А если знаешь как решать, что необходимости в использовании поиска решения для данной задачи нет.
Как решал я:
ГАРАНТИРОВАННЫЙ выигрыш — это тот, который не зависит от вероятностей победы лошадей. Следовательно, ставить нужно на всех лошадей сразу.
Как ставить? Выигрыш от победы лошадей составляет в 2, 3, 7 раз больше внесенной суммы соответственно. Задача минимум: не потерять деньги: ставим на лошадей соответственно 1/2, 1/3, 1/7 часть суммы. Таким образом, независимо от того какая лошадь выигрывает, получаем изначальную сумму, которую берем за 1. Посчитаем какую часть капитала поставили на лошадей: 1/2+1/3+1/7=(21+14+6)/42=41/42. Т. е. остается 1/42 часть суммы. Таким образом, действуя по данной схеме, ГАРАНТИРОВАННО можно получить 1/42 капитала.
Завдання: Визначити згладжене значення функції за методом екстраполяції і побудувати графіки:
а) y = f ( )x – за вихідними даними;
б) y3 = f ( )x – за трьома точками;
в) y5 = f ( )x – за п’ятьома точками.
X 1 2 3 4 5 6 7 8 9 10
Y 24,83 38,38 65,04 120,6 69,38 78,39 69,91 63,89 105,6 89,08
Как решить эту задачу в екселе
Дубликаты ручками покрасили?
задача тяжело пошла …
Задача слишком лёгкая для разбора. Похоже автор математик, но слишком углубился в свои математические дебри. К примеру, слышал что квантовые компьютеры решили задачу века разложить 15 на множители. Это 3 и 5. Ура. Но они не для этого нужны. А теперь к задаче. Я даже для «приколу» посчитаю число действий.
Первое. Нужно сложить все числа, это 1+2+3+4+5+6+7+8 = 36. Справится и калькулятор, потом разделим на 2, так как у нас две суммы должно быть. 36 / 2 = 18. Далее 18 нужно представить из чисел выше от 1 до 8 в единственном экземпляре. Берём наибольшее 8. Итого 18-8 = 10. 10 можно представить как 3 и 7 или 5, 4 и 1, или 1, 2, 3, 4, или 6 и 4. Итого уже накидал 4 оптимальных решения, так как в другой группе так же будет 18 так как эта другая половина. Итого, в одной группе: 3,7,8, далее 1,4,5,8, далее 1,2,3,4 или 4,6,8. Все решения дают 18 в сумме. Итак на эту задачу потратил намного меньше 256 вариантов решения.
Добрый день. Помогите решить задачу по оптимизации посевных площадей. Я так поняла, там нужна функция «поиск решения», но мне выдает ошибку постоянно.
Файл
Где найти другие варианты отчётов после решения. Необходим отчет по устойчивости.