Стандартное отклонение является одним из тех статистических терминов в корпоративном мире, которое позволяет поднять авторитет людей, сумевших удачно ввернуть его в ходе беседы или презентации, и оставляет смутное недопонимание тех, кто не знает, что это такое, но стесняется спросить. На самом деле большинство менеджеров не понимают концепцию стандартного отклонения и, если вы один из них, вам пора перестать жить во лжи. В сегодняшней статье я расскажу вам, как эта недооцененная статистическая мера позволит лучше понять данные, с которыми вы работаете.
Что измеряет стандартное отклонение?
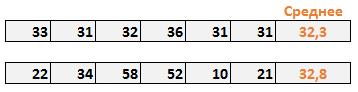
Представьте, что вы владелец двух магазинов. И чтобы избежать потерь, важно, чтобы был четкий контроль остатков на складе. В попытке выяснить, кто из менеджеров лучше управляет запасами, вы решили проанализировать стоки последних шести недель. Средняя недельная стоимость стока обоих магазинов примерно одинакова и составляет около 32 условных единиц. На первый взгляд среднее значение стока показывает, что оба менеджера работают одинаково.
Но если внимательнее изучить деятельность второго магазина, можно убедится, что хотя среднее значение корректно, вариабельность стока очень высокая (от 10 до 58 у.е.). Таким образом, можно сделать вывод, что среднее значение не всегда правильно оценивает данные. Вот где на выручку приходит стандартное отклонение.
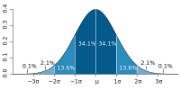
Стандартное отклонение показывает, как распределены значения относительно среднего в нашей выборке. Другими словами, можно понять на сколько велик разброс величины стока от недели к неделе.
В нашем примере, мы воспользовались функцией Excel СТАНДОТКЛОН, чтобы рассчитать показатель стандартного отклонения вместе со средним.
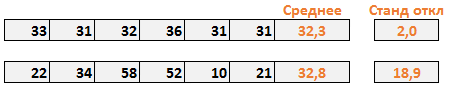
В случае с первым менеджером, стандартное отклонение составило 2. Это говорит нам о том, что каждое значение в выборке в среднем откланяется на 2 от среднего значения. Хорошо ли это? Давайте рассмотрим вопрос под другим углом – стандартное отклонение равное 0, говорит нам о том, что каждое значение в выборке равно его среднему значению (в нашем случае, 32,2). Так, стандартное отклонение 2 ненамного отличается от 0, и указывает на то, что большинство значений находятся рядом со средним значением. Чем ближе стандартное отклонение к 0, тем надежнее среднее. Более того, стандартное отклонение близкое к 0, говорит о маленькой вариабельности данных. То есть, величина стока со стандартным отклонением 2, указывает на невероятную последовательность первого менеджера.
В случае со вторым магазином, стандартное отклонение составило 18,9. То есть стоимость стока в среднем отклоняется на величину 18,9 от среднего значения от недели к неделе. Сумасшедший разброс! Чем дальше стандартное отклонение от 0, тем менее точно среднее значение. В нашем случае, цифра 18,9 указывает на то, что среднему значению (32,8 у.е. в неделю) просто нельзя доверять. Оно также говорит нам о том, что еженедельная величина стока обладает большой вариабельностью.
Такова концепция стандартного отклонения в двух словах. Хотя оно не дает представление о других важных статистических измерениях (Мода, Медиана…), фактически стандартное отклонение играет решающую роль в большинстве статистических расчетов. Понимание принципов стандартного отклонения прольет свет на суть многих процессов вашей деятельности.
Как рассчитать стандартное отклонение?
Итак, теперь мы знаем, о чем говорит цифра стандартного отклонения. Давайте разберемся, как она считается.
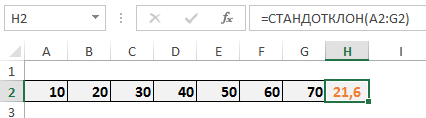
Рассмотрим набор данных от 10 до 70 с шагом 10. Как видите, я уже рассчитал для них значение стандартного отклонения с помощью функции СТАНДОТКЛОН в ячейке H2 (оранжевым).
Ниже описаны шаги, которые предпринимает Excel, чтобы прийти к цифре 21,6.
Обратите внимание, что все расчеты визуализированы, для лучшего понимания. На самом деле в Excel расчет происходит мгновенно, оставляя все шаги за кулисами.
Для начала Excel находит среднее значение выборки. В нашем случае, среднее получилось равным 40, которое на следующем шаге отнимают от каждого значения выборки. Каждую полученную разницу возводят в квадрат и суммируют. У нас получилась сумма равная 2800, которую необходимо разделить на количество элементов выборки минус 1. Так как у нас 7 элементов, получается необходимо 2800 разделить на 6. Из полученного результата находим квадратный корень, это цифра будет стандартным отклонением.
Для тех, кому не совсем ясен принцип расчета стандартного отклонения с помощью визуализации, привожу математическую интерпретацию нахождения данного значения.
Функции расчета стандартного отклонения в Excel
В Excel присутствует несколько разновидностей формул стандартного отклонения. Вам достаточно набрать =СТАНДОТКЛОН и вы сами в этом убедитесь.
Стоит отметить, что функции СТАНДОТКЛОН.В и СТАНДОТКЛОН.Г (первая и вторая функция в списке) дублируют функции СТАНДОТКЛОН и СТАНДОТКЛОНП (пятая и шестая функция в списке), соответственно, которые были оставлены для совместимости с более ранними версиями Excel.
Вообще разница в окончаниях .В и .Г функций указывают на принцип расчета стандартного отклонения выборки или генеральной совокупности. Разницу между двумя этими массивами я уже объяснял в предыдущей статье расчета дисперсии.
Особенностью функций СТАНДОТКЛОНА и СТАНДОТКЛОНПА (третья и четвертая функция в списке), является то, что при расчете стандартного отклонения массива в расчет принимаются логические и текстовые значения. Текстовые и истинные логические значения равняются 1, а ложные логические значения равняются 0. Мне трудно представить ситуацию, когда бы мне могли понадобится эти две функции, поэтому, думаю, что их можно игнорировать.

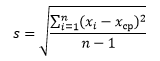

Ренат, добрый день.
Мне нравится статья, а главное способ подачи материала. Визуализация расчёта также порадовала новизной подхода, хотя и времени потребовала больше для понимания (классическое советское образование). Согласен, что про стандартное отклонение никто толком не знает, а зря…
Добрый день.
В формуле ошибка: под знаком корня необходимо суммировать квадраты отклонений
Спасибо, исправил
Спасибо за четкое изложение.
Благодарю за статью! Как раз то что искала!
Спасибо, вы добавили немного ясности в мою работу )))
Спасибо. Недавно читал об этом на английском. А эта статья помогла закрепить материал. Отдельное спасибо за визуализацию рассчетов!
Очень понравилось! Благодарю за труды, куда платить деньги? 🙂
Большое спасибо за информацию в доступном изложении! Оказалась крайне полезной для написания лабораторной работы и помогла упорядочить собственные знания.
Спасибо вам за статью, всё просто и понятно
Вот именно в такой визуальной форме и надо для чайников, как я, писать. Тут никакого текста даже и не надо. А вот по логике я так и не понял. возведение в квадрат разницы от средней, суммирование этих квадратов, деление на кол-во, и вычисление корня. В чем логика — я честно не могу допереть. Какая логика заложена в квадрат разницы и в последующем извлечении корня? Что дает аналитику эта схема вычисления? Я не говорю про общее объяснение, которое приводится в сети, типа «среднее квадратичное отклонение», «максимальный разброс от среднего и т.д.», мне бы логику формулы бы
Возведение в квадрат, а затем извлечение корня из суммы квадратов делается с одной целью, чтобы убрать влияние отрицательных значений. На самом деле вся соль заключается в том, чтобы найти разницу между средним значением массива и конкретным элементом. Грубо — среднее значение этих разниц и является стандартным отклонением
Если не возвести в квадрат отклонения, то сумма всех отклонений всегда будет равна нулю. А это означает, что отклонений типа нет. а они же есть. И чтобы сохранить отклонения и фактически обойти математические правила, отклонения берутся в квадрат.
А чтобы потом обратно приблизиться к реальности, извлекаем результат из под корня. Если квадрат смущает можно использовать формулу среднего линейного отклонения (там вместо квадратов модули берутся)
Здравствуйте. В наглядной иллюстрации в пункте 6 разве не ошибка? 21,6 это «не вся» погрешность, а только половина от нее; нужно отложить 21,6 как в плюс, так и в минус, т.е. если объединять фигурной скобкой, то должно быть 43,2 ?
правильно говорите
Часто вижу в публикациях среднее +_ SD. (хотя выдается _95 +95).
Как правильно?
С м.т. зрения SD — мера размытости, а не +-
запутался
СИ
SD — Standard deviation — переводится, как стандартное отклонение
Доброго дня, есть необходимость исключить из стандартного отклонения 0, как это сделать?
Уточню, среднее отклонение необходимо высчитать из набора цифр, в которых есть 0, этот ноль или нули необходимо исключить при расчетах
мелочь, а очень важно и следовательно выборку надо уменьшить на количество нулевых значений?
Друзья, подскажите, пожалуйста,
1. чем отличается стандартное отклонение от среднего
2. а можно стандартное отклонение выразить в %? к примеру, мы рассчитали, что стандотклон 18,9. Понятно, что это много…. а насколько? проценты так хорошо… Но я никогда не видела, чтобы отклонение выдавали так: стандартное отклонение стока магазина составило 57,6 % (18,9/32,8 * 100%) Теперь действительно видно: «Ого, как много!» Хотя мне для работы удобно говорить, что разница между тремя/пяти результатов лежит в пределах погрешности 6%. Т.е. объясню ситуацию: у меня есть три числа х1=34240, х2=29673, х3=35086. Стандотклон = 2912. Могу я для каждого результата сказать: что отклонение будет % стандотклон/х1 для х1, /х2 для х2 и т.д.?
1. Первое отличие — разные формулы, в среднем линейном отклонении используется модуль и второе отличие — стандартное отклонение считается более точным.
2. Конечно можно в % выразить. Именно % используют в разных отчетах и объяснениях.
Большое спасибо за такое доступное изложение материала, очень помогло понять суть стандартного отклонения
Среднее отклонение данных от среднего значения можно оценить также по функции СРОТКЛ, которая даёт среднее абсолютных значений отклонений данных от среднего значения данных. В статистических расчётах эта функция используется горазд реже, чем СТАНДОТКЛОН
Спасибо большое!
Здравствуйте, я немного запуталась. В книгах по статистике в знаменателе пишут n, а у вас n-1. Можно узнать причину? ведь получается в Exel тоже используется n-1
Об этом написано в статье о дисперсии.
Следовало бы обратить внимение на отношение величины стд отклонения к среднему значению. Если например стандартное отклонение 18 по отношению к среднему 32 означает большой разброс, то 18 к среднему значению 32000 уже небольшоу разброс данных. Другими словами — все относительно.
Шикарно написано, спасибо!!!!
Спасибо! Учусь на английском, было сложно понять этот материал. С Вашей визуализацией все прояснилось! Вы очень помогли!
Спасибо вам большое за статью, очень помогли!
Здравствуйте, я учу этот материал на финском языке. Я все поняла как вычислить среднее отклонение, но что мне это дает? У меня например задача: опрашивают два класса учащихся какой у них размер ноги, в первом классе среднее значение 41,3 , среднее отклонение 1,2, во втором классе соответственно 39,6 и 2,9. Что я могу понять имея эти данные?
Про отклонение написали хорошо, спасибо! А вот пример со складом плохой. В зависимости от сезонности продажи, знаете ли, меняются. И если у первого менеджера, допустим, перед новым годом запасы на стоке +/- равны запасам в 10 числах января — это очень плохой менеджер.
Так непонятно, какой менеджер склада все-таки лучше? Тот кто работает стабильно, но никогда не прыгает выше головы? Или работающий по настроению, но способный выдать результат в два раза выше нормы?
Тоже об этом подумал. Но я так понимаю, главное — найти отличие, а там решат, кого уволить. )) А со средним бы не смогли.
Огромный лайк Вам. Если бы все преподаватели на таких жизненных примерах доносили материал в школах и вузах, уровень образования было бы выше.
Я просто не могу врубиться, почему надо возводить в квадрат, и зачем отнимать единицу для выборки. Жесть.
Спасибо
Спасибо
Pingback: «Как измерить все, что угодно» - Книга кратко за 20 минут - Обзор и 3 отзыва - Купить и читать книгу
Спасибо огромное за объяснение! Столько всего перечитала про отклонение, и вот только все в голове устаканилось наконец! осталось понять, чем отличается стандартное отклонение от дисперсии)) по сути как будто то же самое, только при вычислении дисперсии в конце не используется корень…
https://prokrep.ru