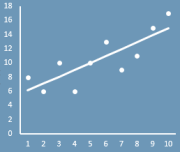
Метод наименьших квадратов — это математическая процедура составления линейного уравнения, максимально соответствующего набору упорядоченных пар, путем нахождения значений для a и b, коэффициентов в уравнении прямой. Цель метода наименьших квадратов состоит в минимизации общей квадратичной ошибки между значениями y и ŷ. Если для каждой точки мы определяем ошибку ŷ, метод наименьших квадратов минимизирует:
где n = число упорядоченных пар вокруг линии. максимально соответствующей данным.
Это понятие проиллюстрировано на рисунке
Судя по рисунку, линия, максимально соответствующая данным, линия регрессии, минимизирует общую квадратичную ошибку четырех точек на графике. Я покажу вам, как определять это уравнение регрессии с помощью метода наименьших квадратов на следующем примере.
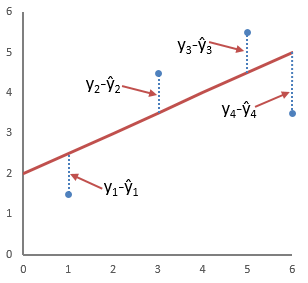
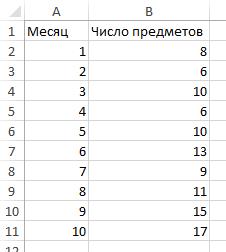
Представьте себе молодую пару, которые, с недавних пор, живут вместе и совместно делят столик для косметических принадлежностей в ванной. Молодой человек начал замечать, что половина его столика неумолимо сокращается, сдавая свои позиции муссам для волос и соевым комплексам. За последние несколько месяцев парень внимательно следил за тем, с какой скоростью увеличивается число предметов на ее части стола. В таблице ниже представлено число предметов девушки на столике в ванной, накопившихся за последние несколько месяцев.
Поскольку своей целью мы определили задачу узнать, увеличивается ли со временем число предметов, «Месяц» будет независимой переменной, а «Число предметов» — зависимой.
С помощью метода наименьших квадратов определяем уравнение, максимально соответствующее данным, путем вычисления значений a, отрезка на оси y, и b, наклона линии:
a = yср — bxср
где xср — среднее значение x, независимой переменной, yср — среднее значение y, независимой переменной.
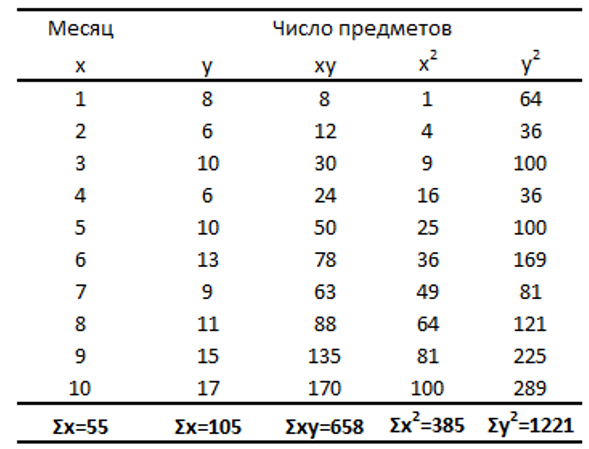
В таблице ниже суммированы необходимые для этих уравнений вычисления.
Кривая эффекта для нашего примера с ванной будет определяться следующим уравнением:
ŷ=5.13+0.976x
Поскольку наше уравнение имеет положительный наклон — 0.976, парень имеет доказательство того, что число предметов на столике со временем увеличивается со средней скоростью 1 предмет в месяц. На графике представлена кривая эффекта с упорядоченными парами.
Ожидание в отношении числа предметов в течение следующего полугода (месяца 16) будет вычисляться так:
ŷ = 5.13 + 0.976x = 5.13 + 0.976(16) ~ 20.7 = 21 предмет
Так что, пора нашему герою предпринимать какие-нибудь действия.
Функция ТЕНДЕНЦИЯ в Excel
Как вы уже, наверное, догадались в Excel имеется функция для расчета значения по методу наименьших квадратов. Это функция называется ТЕНДЕНЦИЯ. Синтаксис у нее следующий:
ТЕНДЕНЦИЯ (известные значения Y; известные значения X; новые значения X; конст)
где:
известные значения Y – массив зависимых переменных, в нашем случае, количество предметов на столике
известные значения X – массив независимых переменных, в нашем случае это месяц
новые значения X – новые значения X (месяца) для которого функция ТЕНДЕНЦИЯ возвращает ожидаемое значение зависимых переменных (количество предметов)
конст — необязательный. Логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0.
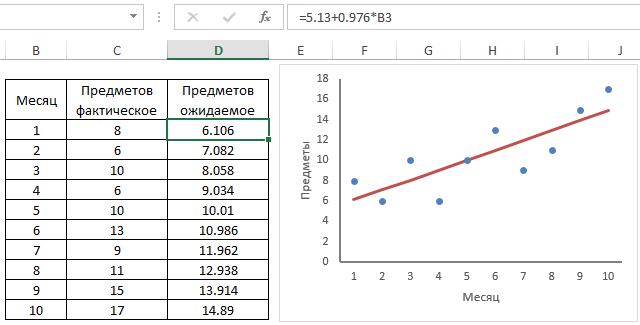
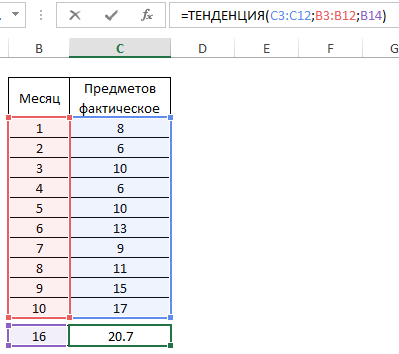
Например, на рисунке показана функция ТЕНДЕНЦИЯ, используемая для определения ожидаемого количества предметов на столике в ванной для 16-го месяца.
Скачать файл с примером расчета значений по методу наименьших квадратов
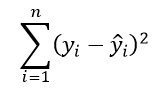
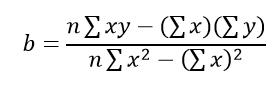
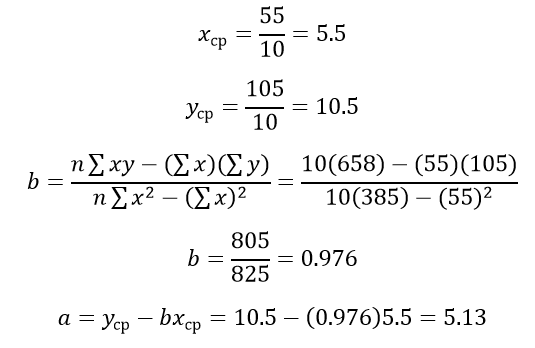
Спасибо большое, очень интересное объяснение!
Скажите Ренат, а можно использовать «Тенденцию» в лото.
мой мейл — horizont999@yahoo.com
Спасибо.
Нет, но попытаться все таки стоит, вдруг повезет)
Джимшер — нет возможности предсказывать независимые события. Даже если при броске монеты решка будет выпадать несколько раз — это не значит что она выпадет снова, конечно если это не специальная монета
На счёт монеты — я имел в виду выпадение решки несколько раз подряд.
Вопрос, я ведь могу в качестве аргумента x использовать множество столбцов. Как в этом случае будет реагировать данная функция. Например, если за еще один параметр я возьму день недели?
Даа точно, у меня точно такой же вопрос, а что если не зависимых параметров не один а несколько…. если найдете в пространствах интернета дайте знать… буду весьма благодарен…
«Так что, пора нашему герою предпринимать какие-нибудь действия»- прям лирика какая-то… Т.с. Excel для блондинок.
И чё?