
Дисперсия — это мера рассеяния, описывающая сравнительное отклонение между значениями данных и средней величиной. Является наиболее используемой мерой рассеяния в статистике, вычисляемая путем суммирования, возведенного в квадрат, отклонения каждого значения данных от средней величины. Формула для вычисления дисперсии представлена ниже:
где:
s2 – дисперсия выборки;
xср — среднее значение выборки;
n — размер выборки (количество значений данных),
(xi – xср) — отклонение от средней величины для каждого значения набора данных.
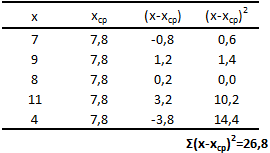
Для лучшего понимания формулы, разберем пример. Я не очень люблю готовку, поэтому занятием этим занимаюсь крайне редко. Тем не менее, чтобы не умереть с голоду, время от времени мне приходится подходить к плите для реализации замысла по насыщению моего организма белками, жирами и углеводами. Набор данных, редставленный ниже, показывает, сколько раз Ренат готовит пищу каждый месяц:
Первым шагом при вычислении дисперсии является определение среднего значения выборки, которое в нашем примере равняется 7,8 раза в месяц. Остальные вычисления можно облегчить с помощью следующей таблицы.
Финальная фаза вычисления дисперсии выглядит так:
Для тех, кто любит производить все вычисления за один раз, уравнение будет выглядеть следующим образом:
Использование метода «сырого счета» (пример с готовкой)
Существует более эффективный способ вычисления дисперсии, известный как метод «сырого счета». Хотя с первого взгляда уравнение может показаться весьма громоздким, на самом деле оно не такое уж страшное. Можете в этом удостовериться, а потом и решите, какой метод вам больше нравится.
где:
![]() — сумма каждого значения данных после возведения в квадрат,
— сумма каждого значения данных после возведения в квадрат,
![]() — квадрат суммы всех значений данных.
— квадрат суммы всех значений данных.
Не теряйте рассудок прямо сейчас. Позвольте представить все это в виде таблицы, и тогда вы увидите, что вычислений здесь меньше, чем в предыдущем примере.
Как видите, результат получился тот же, что и при использовании предыдущего метода. Достоинства данного метода становятся очевидными по мере роста размера выборки (n).
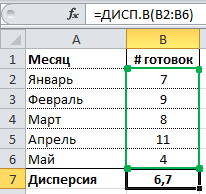
Расчет дисперсии в Excel
Как вы уже, наверное, догадались, в Excel присутствует формула, позволяющая рассчитать дисперсию. Причем, начиная с Excel 2010 можно найти 4 разновидности формулы дисперсии:
1) ДИСП.В – Возвращает дисперсию по выборке. Логические значения и текст игнорируются.
2) ДИСП.Г — Возвращает дисперсию по генеральной совокупности. Логические значения и текст игнорируются.
3) ДИСПА — Возвращает дисперсию по выборке с учетом логических и текстовых значений.
4) ДИСПРА — Возвращает дисперсию по генеральной совокупности с учетом логических и текстовых значений.
Для начала разберемся в разнице между выборкой и генеральной совокупностью. Назначение описательной статистики состоит в том, чтобы суммировать или отображать данные так, чтобы оперативно получать общую картину, так сказать, обзор. Статистический вывод позволяет делать умозаключения о какой-либо совокупности на основе выборки данных из этой совокупности. Совокупность представляет собой все возможные исходы или измерения, представляющие для нас интерес. Выборка — это подмножество совокупности.
Например, нас интересует совокупность группы студентов одного из Российских ВУЗов и нам необходимо определить средний бал группы. Мы можем посчитать среднюю успеваемость студентов, и тогда полученная цифра будет параметром, поскольку в наших расчетах будет задействована целая совокупность. Однако, если мы хотим рассчитать средний бал всех студентов нашей страны, тогда эта группа будет нашей выборкой.
Разница в формуле расчета дисперсии между выборкой и совокупностью заключается в знаменателе. Где для выборки он будет равняться (n-1), а для генеральной совокупности только n.
Теперь разберемся с функциями расчета дисперсии с окончаниями А, в описании которых сказано, что при расчете учитываются текстовые и логические значения. В данном случае при расчете дисперсии определенного массива данных, где встречаются не числовые значения, Excel будет интерпретировать текстовые и ложные логические значения как равными 0, а истинные логические значения как равными 1.
Итак, если у вас есть массив данных, рассчитать его дисперсию ни составит никакого труда, воспользовавшись одной из перечисленных выше функций Excel.
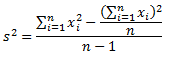
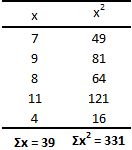
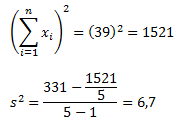
Спасибо. Очень хорошие, простые объяснения и примеры!
Здравствуйте хотел узнать правельно ли я решил задачу
Файл: 1-—-копия.xlsx
Приятно, что кто-то умеет излагать сложные вещи доступным языком… Можете объяснить начинающему любителю Excel практическую разницу между стандартным отклонением и дисперсией? Вроде бы и то и то указывает отклонение от среднего значения… Спасибо!
Легко заметить, что стандартное отклонение — это корень от дисперсии. Разница в том, что дисперсия это наиболее вероятный разброс между максимальным и минимальным значениями, которые принимает функция. А ст. Отклонение определяет точность среднего значения. На практике, например, дисперсия поможет определить уровень требуемого остатка товара, а ср. Отклонение оценить качество планирования по итогу. Как-то так.
Спасибо большое, Ренат, мне очень помог. Можешь показать Анова, one way, two way, multifactoral Anova?
Ренат, спасибо большое! Мне очень понравилось как Вы излагаете материал.
Спасибо
Я обычно не пишу комментарии, но в данном случае просто не могу удержаться. Ренат, спасибо огромное за такое детальное, понятное и простое объяснение! Я в статистике — ноль, и мне с гуманитарным складом ума очень тяжело это понять. А на всех сайтах нас загружают какой-то непонятной информацией с огромными страшными формулами и таким же их описанием. НО, не говорят самое важное — на какую кнопку нужно жать.
У вас же есть все — и те же формулы, но к ним понятное описание. И четкое описание работы с программой. Спасибо большое за ваш труд!
Большое спасибо, Ренат. Пожалуйста, продолжайте делать то, что вы делаете.
у вас ошибка или как? в таблице среднее 7,8, а в вычислениях ниже среднее взято как 7,7.
Не понятен физический смысл величин. Например, в среднем Ренат готовит 7.8 раз в месяц. Тогда что показывает дисперися равная 6.7?
откуда взялось 7,8? . Подскажите пожалуйста, а то что-то не пойму.
Жму Вам руку двумя кистями. Внесли ясность и понимание. Благодарю.